1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 | #include <iostream> #include <cstdio> #include <vector> #include <string> #include <deque> #include <algorithm> using namespace std; int calculate(int n1, int n2, char op) { switch (op) { case '+': return n1 + n2; break; case '-': return n1 - n2; break; case 'x': return n1 * n2; break; case '/': return n1 / n2; break; } return -1; } bool solve(string s) { deque<int> si; deque<char> sop; for (int i = 0; i < 7; i++) { if (i % 2 == 0) { // Inttop int t = s[i] - '0'; si.push_back(t); if (sop.empty()) continue; if (sop.back() == 'x' || sop.back() == '/') { int t2 = si.back(); si.pop_back(); int t1 = si.back(); si.pop_back(); int t = calculate(t1, t2, sop.back()); sop.pop_back(); si.push_back(t); } } else { // Op char op = s[i]; sop.push_back(op); } } while (!sop.empty()) { int t1 = si.front(); si.pop_front(); int t2 = si.front(); si.pop_front(); int t = calculate(t1, t2, sop.front()); sop.pop_front(); si.push_front(t); } return si.front()==24; } int main() { ios::sync_with_stdio(false); int n; string s; cin >> n; while (n--) { cin >> s; if (solve(s)) cout << "Yes\n"; else cout << "No\n"; } } |
分类目录归档:栈
Openjudge BJUTACM 19g系列代码
题目链接:
http://bjutacm.openjudge.cn/lianxi/?page=2
蓝桥杯 历届试题 小计算器
问题描述
模拟程序型计算器,依次输入指令,可能包含的指令有
1. 数字:’NUM X’,X为一个只包含大写字母和数字的字符串,表示一个当前进制的数
2. 运算指令:’ADD’,’SUB’,’MUL’,’DIV’,’MOD’,分别表示加减乘,除法取商,除法取余
3. 进制转换指令:’CHANGE K’,将当前进制转换为K进制(2≤K≤36)
4. 输出指令:’EQUAL’,以当前进制输出结果
5. 重置指令:’CLEAR’,清除当前数字
指令按照以下规则给出:
数字,运算指令不会连续给出,进制转换指令,输出指令,重置指令有可能连续给出
运算指令后出现的第一个数字,表示参与运算的数字。且在该运算指令和该数字中间不会出现运算指令和输出指令
重置指令后出现的第一个数字,表示基础值。且在重置指令和第一个数字中间不会出现运算指令和输出指令
进制转换指令可能出现在任何地方
运算过程中中间变量均为非负整数,且小于2^63。
以大写的’A’~’Z’表示10~35
输入格式
第1行:1个n,表示指令数量
第2..n+1行:每行给出一条指令。指令序列一定以’CLEAR’作为开始,并且满足指令规则
输出格式
依次给出每一次’EQUAL’得到的结果
样例输入
7
CLEAR
NUM 1024
CHANGE 2
ADD
NUM 100000
CHANGE 8
EQUAL
样例输出
2040
可以说样例给的挺恶心。会让人想不到,这玩意要考虑还是不考虑优先级!?最后在测试下是不需要考虑优先级的。直接挨着个的算即可。还有一个点是我进制转换写错了(竟然’A’->11,生无可恋脸)一直在调这里。。。。其他没啥了。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 | #include<iostream> #include<deque> #include<algorithm> #include<cassert> #include<cstdlib> #include<string> using namespace std; int n; int radix = 10; string radixS = "0123456789ABCDEFGHIJKLMNOPQRSTUVWXYZ"; deque<long long> sll; deque<string> sop; long long value; inline long long getCorDecimal(char c) { if ('0' <= c && c <= '9')return c - '0'; if ('A' <= c && c <= 'Z')return c - 'A' + 10; assert(false); return -1; } long long Radix2Decimal(string s) { reverse(s.begin(), s.end()); long long cntBase = 1, result = 0; for (int i = 0; i<s.size(); i++) { result += getCorDecimal(s[i])*cntBase; cntBase *= radix; } return result; } string Decimal2Radix(long long v) { string s = ""; while (v) { s.push_back(radixS[v%radix]); v /= radix; } if (s == "")s = "0"; reverse(s.begin(), s.end()); return s; } bool calculate4Back() { if (sop.empty())return false; string & comm = sop.back(); if (comm == "ADD")value += sll.back(); else if (comm == "SUB")value = sll.back() - value; else if (comm == "MUL")value *= sll.back(); else if (comm == "DIV")value = sll.back() / value; else if (comm == "MOD")value = sll.back() % value; else assert(false); sop.pop_back(); sll.pop_back(); sll.push_back(value); return true; } int main() { ios::sync_with_stdio(false); cin.tie(0); cin >> n; for (int i = 1; i <= n; i++) { string comm, radixV; cin >> comm; if (comm == "NUM") { cin >> radixV; value = Radix2Decimal(radixV); if (!calculate4Back())sll.push_back(value); //cout<<Decimal2Radix(sll.front())<<endl; } else if (comm == "ADD" || comm == "SUB" || comm == "MUL" || comm == "DIV" || comm == "MOD") { sop.push_back(comm); } else if (comm == "CHANGE") { cin >> radix; } else if (comm == "EQUAL") { cout << Decimal2Radix(sll.front()) << endl; } else if (comm == "CLEAR") { sll.clear(); sop.clear(); } } } |
Openjudge BJUTACM 2018 周末集训 1005:Largest Rectangle in a Histogram
可以说是非常不好想也非常不好做的一道题了……大佬的提示是单调栈,自己随便想了想就开始写,结果就挂掉了,然后看题解,也没太大用,最后是单步调试让我差不多搞清楚了。Solve()函数里的每一行都博大精深,有很多用。我也实在讲不清楚,把AC代码发上来,再贴几个题解连接参考一下吧。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 | #include<cstdio> #include<stack> #include<vector> #include<algorithm> using namespace std; long long solve(vector<long long> & heights) { long long remax = 0; stack<long long> spos; heights.push_back(0); for (int i = 0; i < heights.size(); i++) { while (!spos.empty() && heights[spos.top()] >= heights[i]) { int curpos = spos.top(); spos.pop(); remax = max(remax, heights[curpos] * (spos.empty() ? i : ((i - 1) - (spos.top() + 1) + 1))); //这里大部分题解写的是i-spos.top()-1,我搞明白之后把这里写成了易于理解的形式 } spos.push(i); } return remax; } int main() { do { int n; scanf("%d", &n); if (n == 0)break; vector<long long> v; for (int i = 1; i <= n; i++) { long long x; scanf("%lld", &x); v.push_back(x); } printf("%lld", solve(v)); } while (1); } |
此题为LeetCode原题:https://leetcode.com/problems/largest-rectangle-in-histogram/description/
该题BJUTACM地址:http://bjutacm.openjudge.cn/bjut2018/1005/
(数据范围有可能会不相同)
题解:
https://www.cnblogs.com/grandyang/p/4322653.html
https://blog.csdn.net/princexiexiaofeng/article/details/79652003
https://siddontang.gitbooks.io/leetcode-solution/content/array/largest_rectangle_in_histogram.html
https://tech.pic-collage.com/algorithm-largest-area-in-histogram-84cc70500f0c
我个人看题解是没看懂的,单步调试拯救了我。。如果看不懂就单步吧。。有的地方我没解释清楚,从网上搜搜题解就好。
强烈建议这道题单步跟,多跟几个样例,不单步你看不懂其中的逻辑。。
我按照雪花大佬做法写的,经我垃圾的改编加了一堆cruft:不要问我怎么回事我也搞不清楚
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 | #include<cstdio> #include<stack> #include<vector> #include<algorithm> using namespace std; struct P { long long h, i; }; long long solve(vector<long long> & heights) { long long remax = 0; stack<P> s; heights.push_back(0); for (int i = 0; i < heights.size(); i++) { long long l = i; while (!s.empty() && s.top().h > heights[i]){ l = s.top().i; remax = max(remax, s.top().h * ( (i - 1) - s.top().i + 1)); s.pop(); } s.push(P{ heights[i],l }); } return remax; } int main() { do { int n; scanf("%d", &n); if (n == 0)break; vector<long long> v; for (int i = 1; i <= n; i++) { long long x; scanf("%lld", &x); v.push_back(x); } printf("%lld\n", solve(v)); } while (1); } |
雪花大佬的不cruft的代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 | #include <iostream> #include <algorithm> using namespace std; using ll = long long; struct Candidate { // candidate rectangle. area = height * (end_pos - start_pos) ll h; // the height ll i; // the start position; // end position is implied }; Candidate monostack[100100]; ll size = 0; ll max_area = 0; void monostack_push(ll h, ll i) { ll pos = i; // start pos while (size > 0 && monostack[size - 1].h >= h) { // equality is optional Candidate const & p = monostack[--size]; // pop pos = p.i; // update start pos max_area = max(max_area, p.h * (i - p.i)); } monostack[size++] = {h, pos}; // push } int main() { // init size = 0; max_area = 0; // for each input // monostack_push(height, pos); // monostack_push(0, last pos + 1); // another trick // output max_area } |
Openjudge BJUTACM 1036:括号画家
智障的一开始竟然想用递归/记忆化做。。。老T。后来猛然醒悟是栈。。。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 | #define _CRT_SECURE_NO_WARNINGS #include<iostream> #include<algorithm> #include<cstdio> #include<cstring> #include<string> #include<stack> #include<vector> #include<typeinfo> using namespace std; void E() { cout << "No"; exit(0); } void S() { cout << "Yes"; exit(0); } stack<char> s; int main() { char c; while (cin >> c) { switch (c) { case '(':case '[':case '{': s.push(c); break; case ')':case ']':case '}': if (s.empty())E(); switch (c) { case ')': if (s.top() == '(')s.pop(); else E(); break; case ']': if (s.top() == '[')s.pop(); else E(); break; case '}': if (s.top() == '{')s.pop(); else E(); break; } } } S(); } |
http://bjutacm.openjudge.cn/lianxi/1036/
Openjudge BJUTACM 1018:简单计算器
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 | #define _CRT_SECURE_NO_WARNINGS #include<iostream> #include<algorithm> #include<cstdio> #include<cstring> #include<stack> #include<vector> #include<typeinfo> using namespace std; int t; stack<double> si; stack<char> sc; inline bool execute() { if (sc.empty()) return false; double x2 = si.top(); si.pop(); double x1 = si.top(); si.pop(); char symbol = sc.top(); sc.pop(); switch (symbol) { case '+':si.push(x1 + x2); break; case '-':si.push(x1 - x2); break; case '*':si.push(x1 * x2); break; case '/':si.push(x1 / x2); break; } return true; } int main() { scanf("%d", &t); do { char c = getc(stdin); if (c == -1)break; if (c == '\n') { while (execute()); if (si.empty())continue; double v = si.top(); while (!si.empty())si.pop(); while (!sc.empty())sc.pop(); printf("%.2lf\n", v); continue; } if (c <= '9' && c >= '0') { ungetc(c, stdin); double v; scanf("%lf", &v); if (sc.empty())si.push(v); else if (sc.top() == '-') { si.push(-v); sc.pop(); sc.push('+'); } else if (sc.top() == '/') { si.push(1.0 / v); sc.pop(); sc.push('*'); } else si.push(v); } else if (c == '+' || c == '-' || c == '*' || c == '/') { while (!sc.empty() && (c == '+' || c == '-') && (sc.top() == '*' || sc.top() == '/')) { execute(); } sc.push(c); } } while (1); } |
http://bjutacm.openjudge.cn/lianxi/1018/
THU2017spring 2-2 Train 题解
THU2017spring 2-2 Train
描述
某列车调度站的铁道联接结构如图所示。
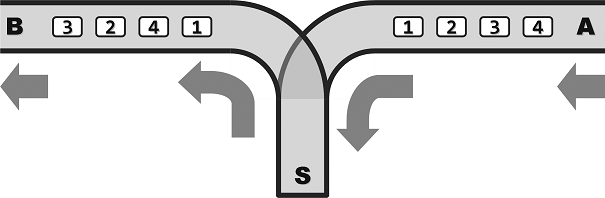
其中,A为入口,B为出口,S为中转盲端。所有铁道均为单轨单向式:列车行驶的方向只能是从A到S,再从S到B;另外,不允许超车。因为车厢可在S中驻留,所以它们从B端驶出的次序,可能与从A端驶入的次序不同。不过S的容量有限,同时驻留的车厢不得超过m节。
设某列车由编号依次为{1, 2, …, n}的n节车厢组成。调度员希望知道,按照以上交通规则,这些车厢能否以{a1, a2, …, an}的次序,重新排列后从B端驶出。
输入
共两行。
第一行为两个整数n,m。
第二行为以空格分隔的n个整数,保证为{1, 2, …, n}的一个排列,表示待判断可行性的驶出序列{a1,a2,…,an}。
输出
仅一行。若驶出序列可行,则输出Yes;否则输出No。
输入样例1
5 2
1 2 3 5 4
输出样例1
Yes输入样例2
5 5
3 1 2 4 5
输出样例2
No限制
1 <= n <= 100,000
0 <= m <= 100,000
时间:1 sec
空间:256 MB
提示
无
这题边界条件比MOOC卡的严多了,需要考虑0的情况:
也是栈混洗,把原来的代码搞过来的……(逃)
继续阅读
数据结构 邓俊辉 PA#2 列车调度(Train) 题解
Description
Figure 1 shows the structure of a station for train dispatching.

Figure 1
In this station, A is the entrance for each train and B is the exit. S is the transfer end. All single tracks are one-way, which means that the train can enter the station from A to S, and pull out from S to B. Note that the overtaking is not allowed. Because the compartments can reside in S, the order that they pull out at B may differ from that they enter at A. However, because of the limited capacity of S, no more that m compartments can reside at S simultaneously.
Assume that a train consist of n compartments labeled {1, 2, …, n}. A dispatcher wants to know whether these compartments can pull out at B in the order of {a1, a2, …, an} (a sequence). If can, in what order he should operate it?
Input
Two lines:
1st line: two integers n and m;
2nd line: n integers separated by spaces, which is a permutation of {1, 2, …, n}. This is a compartment sequence that is to be judged regarding the feasibility.
Output
If the sequence is feasible, output the sequence. “Push” means one compartment goes from A to S, while “pop” means one compartment goes from S to B. Each operation takes up one line.
If the sequence is infeasible, output a “no”.
Example 1
Input
5 2
1 2 3 5 4
Output
push
pop
push
pop
push
pop
push
push
pop
pop
Example 2
Input
5 5
3 1 2 4 5
Output
No
Restrictions
1 <= n <= 1,600,000
0 <= m <= 1,600,000
Time: 2 sec
Memory: 256 MB
描述
某列车调度站的铁道联接结构如Figure 1所示。
其中,A为入口,B为出口,S为中转盲端。所有铁道均为单轨单向式:列车行驶的方向只能是从A到S,再从S到B;另外,不允许超车。因为车厢可在S中驻留,所以它们从B端驶出的次序,可能与从A端驶入的次序不同。不过S的容量有限,同时驻留的车厢不得超过m节。
设某列车由编号依次为{1, 2, …, n}的n节车厢组成。调度员希望知道,按照以上交通规则,这些车厢能否以{a1, a2, …, an}的次序,重新排列后从B端驶出。如果可行,应该以怎样
的次序操作?
输入
共两行。
第一行为两个整数n,m。
第二行为以空格分隔的n个整数,保证为{1, 2, …, n}的一个排列,表示待判断可行性的驶出序列{a1,a2,…,an}。
输出
若驶出序列可行,则输出操作序列,其中push表示车厢从A进入S,pop表示车厢从S进入B,每个操作占一行。
若不可行,则输出No。
样例
见英文题面
限制
1 ≤ n ≤ 1,600,000
0 ≤ m ≤ 1,600,000
时间:2 sec
空间:256 MB