日度归档：30 7 月, 2017

计蒜客 NOIP模拟赛（一） D1T2

发表评论

原题：https://nanti.jisuanke.com/t/16446
北京市八十中的cjr说（特别感谢cjr提供思路，我进行了一下整理）：考虑每条边对答案的贡献：每条边肯定是一个父亲节点与一个儿子节点相连，该边对答案的贡献是size[i]*(n-size[i])*w，其中i为儿子节点，size[i]为该边的儿子节点所对应的子树大小（包括该儿子节点），w[i]为边权，n为总节点数。可以这样做是利用了乘法原理。想象一下，假设一棵有根树，要计算从Node:n到其它所有节点的最短距离：

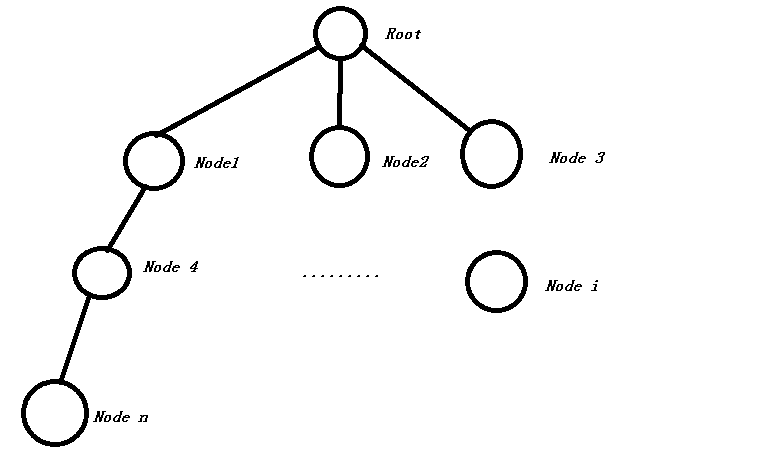
该边必然要使用1*(n-1)次，该边对答案的贡献就为1*(n-1)*w[i]了。
子树大小由dfs算得即可，因为这是有根树。如果是图的话就不能这么干了，因为两个节点之间不仅仅又1条路径，这时候多源最短路只能用floyd做了。时间复杂度为O(n^3)。
本题第一次计算任意两点间距离之和：初始化子树大小DFS复杂度O(n)，算每条边的贡献O(n)，更改边长复杂度O(1)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
#include<iostream>
#include<list>
using namespace std;
int n,m;
long long father[100005],w[100005];
list<int> children[100005];
long long treesize[100005];
void dfs(int node){//获得子树大小
    if(children[node].size()==0){
        treesize[node]=1;
        return;
    }
    long long tot=0;
    for(list<int>::iterator i=children[node].begin();i!=children[node].end();i++){
        dfs(*i);
        tot+=treesize[*i];
    }
    treesize[node]=tot+1;
    return;
}
int main(){
    ios::sync_with_stdio(false);
    cin>>n;
    for(int i=2;i<=n;i++){
        cin>>father[i]>>w[i];
        children[father[i]].push_back(i);
    }
    dfs(1);
    long long tot=0;
    for(int i=2;i<=n;i++){
        tot+=treesize[i]*(n-treesize[i])*w[i];
    }
    cout<<tot<<endl;
    cin>>m;
    for(int i=1;i<=m;i++){
        int a,b;
        cin>>a>>b;
        long long change=treesize[a]*(n-treesize[a])*(b-w[a]);
        tot+=change;
        cout<<tot<<endl;
        w[a]=b;
    }
}